adminC++常用算法2024-07-25

C++ 排序算法（基本）

C++ 常见的排序算法包括如下：

冒泡排序（Bubble Sort）
选择排序（Selection Sort）
插入排序（Insertion Sort）
希尔排序（Shell Sort）
归并排序（Merge Sort）
快速排序（Quick Sort）
堆排序（Heap Sort）
计数排序（Counting Sort）
桶排序（Bucket Sort）
基数排序（Radix Sort）

冒泡排序

void bubbleSort(vector<int>& vec) {
    int n = vec.size();
    for (int i = 0; i < n-1; i++) {
        for (int j = 0; j < n-i-1; j++) {
            if (vec[j] > vec[j+1]) {
                // 交换 vec[j] 和 vec[j+1]
                int temp = vec[j];
                vec[j] = vec[j+1];
                vec[j+1] = temp;
            }
        }
    }
}

比较相邻元素： 从数组的第一个元素开始，依次比较相邻的两个元素。
交换位置： 如果前面的元素大于后面的元素（如果是升序排序），则交换它们的位置，将较大的元素向后移动。
重复步骤1和2： 继续执行以上步骤，直到数组末尾，这样一次遍历后，数组中最大的元素将会放置到末尾位置。
减少遍历范围： 在第一次遍历完成后，最大的元素已经就位，接下来的遍历不需要考虑已经排序好的元素，因此每次遍历时可以减少遍历的范围。
重复多次遍历： 重复执行以上步骤，每次遍历后，未排序部分的范围缩小，直到整个数组都被排序。

这样通过多次遍历数组，每次遍历都会将一个最大（或最小）的元素放到合适的位置，直到整个数组有序。

最坏时间复杂度：O(N^2)

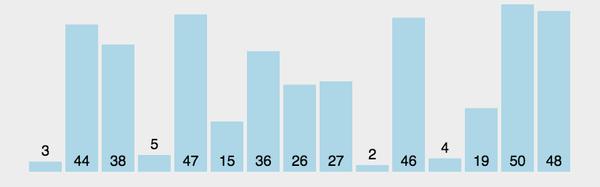
选择排序

初始状态： 首先，将待排序的数组分为两部分：已排序部分和未排序部分。初始时，已排序部分为空，整个数组都是未排序部分。
选择最小元素： 在未排序部分中找到最小的元素，并记录其下标。
交换位置： 将找到的最小元素与未排序部分的第一个元素进行交换，即将最小元素放到已排序部分的末尾。
增加已排序部分： 将已排序部分的末尾指针向后移动一个位置，表示已排序部分增加了一个元素。
重复步骤2到4： 重复执行以上步骤，直到未排序部分为空，即所有元素都已经放到已排序部分，排序完成。

这种算法的关键在于每次在未排序部分中选择最小的元素放到已排序部分的末尾，通过不断地增加已排序部分的长度来完成排序。选择排序的时间复杂度为 O(n^2)，因为它在每个元素的位置上执行了一个最小值查找。虽然选择排序的时间复杂度较高，但是由于它的实现简单，对于小规模的数据集是一个有效的排序算法。

void selectionSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = 0; i < n-1; i++) {
        int minIndex = i;
        for (int j = i+1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        // 交换 arr[i] 和 arr[minIndex]
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

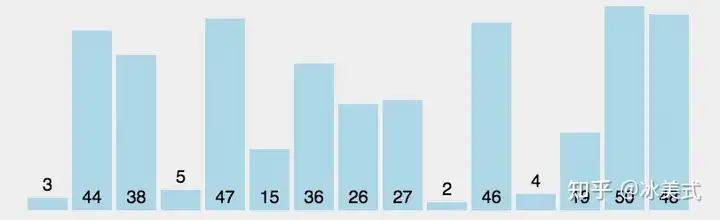
插入排序

初始状态： 将数组视为两部分，已排序部分和未排序部分。初始时，已排序部分只有第一个元素，而剩余部分是未排序的。
逐个插入： 从第二个元素开始，逐个将未排序部分的元素插入到已排序部分中合适的位置。
比较并移动： 将当前要插入的元素与已排序部分的元素从后往前逐个比较，如果已排序部分的元素比当前元素大，则将已排序部分的元素向后移动一位，直到找到当前元素应该插入的位置。
插入元素： 将当前元素插入到已排序部分的合适位置。
重复步骤2到4： 重复执行以上步骤，直到所有元素都被插入到已排序部分，数组排序完成。

插入排序的时间复杂度为 O(n^2)，它比冒泡排序和选择排序更高效，尤其是在处理小规模数据集时。

void insertionSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = 1; i < n; i++) {
        int key = arr[i]; // 当前要插入的元素
        int j = i - 1; // 已排序部分的最后一个元素的下标

        // 将大于 key 的元素向后移动
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        
        // 插入 key 到合适的位置
        arr[j + 1] = key;
    }
}

希尔排序

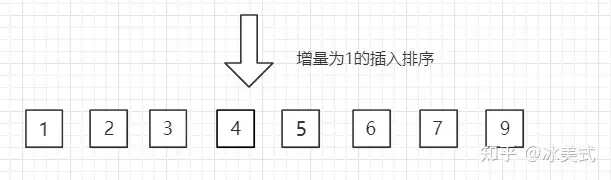
选择增量序列： 希尔排序是插入排序的改进版，它通过定义一个增量序列来对数组进行分组，初始时，增量序列设定为数组长度的一半，然后逐步缩小增量直到为1。
分组插入排序： 对每个增量进行插入排序，这里不是简单地将一个元素插入到已排序部分中，而是将元素按照步长分组，然后对每个分组进行插入排序。
插入排序： 对每个分组进行插入排序，即对每个分组中的元素进行插入排序，这样可以加快插入排序的速度，因为增量较大时，每个分组中的元素数量相对较少。
逐步缩小步长： 重复以上步骤，逐步缩小增量，直到增量为1，此时就是最后一次插入排序，整个数组排序完成。

希尔排序的时间复杂度取决于增量序列的选择，一般情况下，其时间复杂度介于 O(n) 和 O(n^2) 之间，相对于简单的插入排序来说，希尔排序在处理大规模数据时有更好的性能表现。

#include <iostream>
#include <vector>
using namespace std;

void shellSort(vector<int>& arr) {
    int n = arr.size();
    // 初始步长设为数组长度的一半，然后逐步缩小步长直到为1
    for (int gap = n / 2; gap > 0; gap /= 2) {
        // 对每个步长进行插入排序
        for (int i = gap; i < n; i++) {
            int temp = arr[i];
            int j;
            // 对每个分组进行插入排序
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                arr[j] = arr[j - gap];
            }
            arr[j] = temp;
        }
    }
}

int main() {
    vector<int> arr = {64, 34, 25, 12, 22, 11, 90};
    
    cout << "原始数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;
    
    shellSort(arr);
    
    cout << "排序后的数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;
    
    return 0;
}

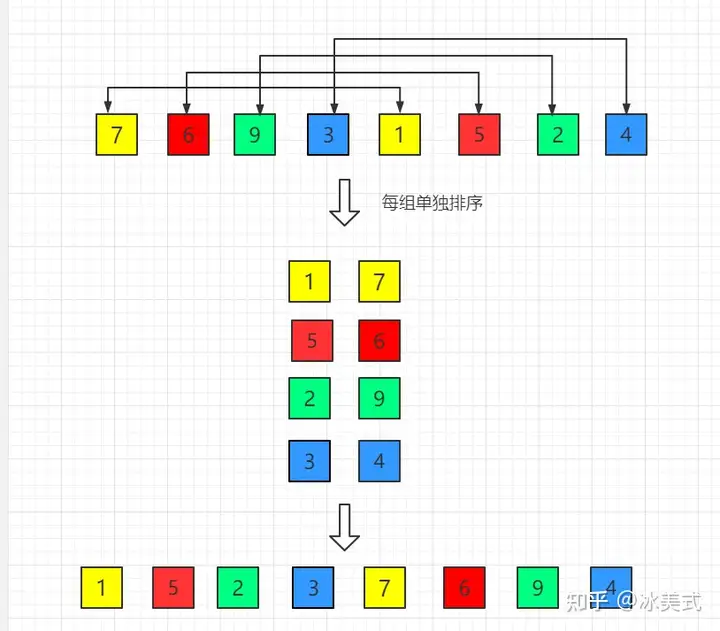
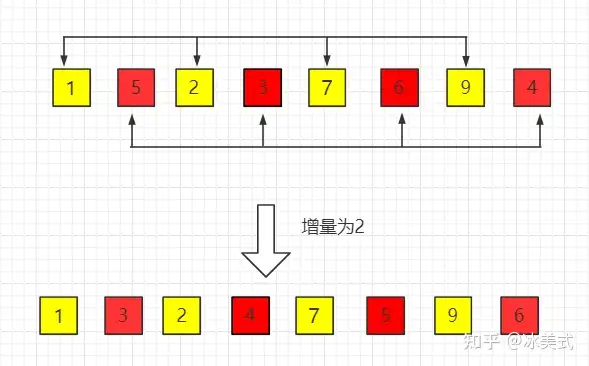
归并排序

分解： 将数组递归地分解为越来越小的子数组，直到子数组的长度为1，此时认为这些子数组都是有序的。
合并： 将两个有序的子数组合并成一个有序的数组。合并过程中，创建一个临时数组，然后按照顺序比较两个子数组的元素，将较小的元素放入临时数组中。
递归合并： 重复以上步骤，直到所有子数组都合并为一个完整的有序数组。

归并排序的时间复杂度为 O(n log n)，其中 n 是数组的大小。归并排序是一种稳定的排序算法，适用于各种数据规模，并且相对于其他复杂度为 O(n log n) 的排序算法而言，归并排序有着较好的稳定性和可靠性。

#include <iostream>
#include <vector>
using namespace std;

void merge(vector<int>& arr, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;

    // 创建临时数组来存储左右子数组
    vector<int> L(n1), R(n2);
    
    // 将数据复制到临时数组中
    for (int i = 0; i < n1; i++)
        L[i] = arr[left + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[mid + 1 + j];

    // 合并临时数组
    int i = 0, j = 0, k = left;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // 处理剩余的元素
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

void mergeSort(vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        // 递归地对左右两部分进行排序
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        // 合并已排序的左右两部分
        merge(arr, left, mid, right);
    }
}

int main() {
    vector<int> arr = {64, 34, 25, 12, 22, 11, 90};
    
    cout << "原始数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;
    
    mergeSort(arr, 0, arr.size() - 1);
    
    cout << "排序后的数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;
    
    return 0;
}

快速排序

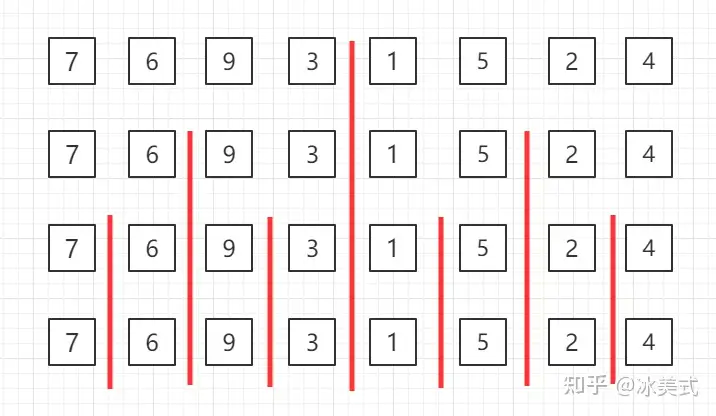
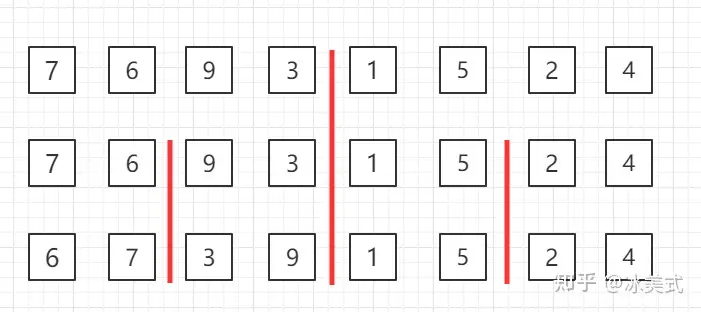
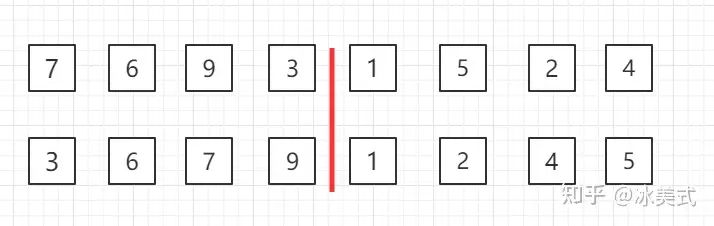
选择基准值： 从数组中选择一个元素作为基准值。通常选择最后一个元素作为基准值，但也可以选择随机位置或者中间位置的元素。
划分数组： 将数组分成两个子数组，其中一个子数组的所有元素都小于基准值，另一个子数组的所有元素都大于或等于基准值。
递归排序： 递归地对两个子数组进行快速排序。
合并结果： 由于快速排序是原地排序算法，所以不需要显式合并子数组。整个数组在递归调用结束后已经被排序好了。

快速排序的平均时间复杂度为 O(n log n)，最坏情况下的时间复杂度为 O(n^2)，其中 n 是数组的大小。虽然最坏情况下的时间复杂度较高，但是快速排序通常被认为是最快的排序算法之一，特别是对于大规模数据集。

#include <iostream>
#include <vector>
using namespace std;

int partition(vector<int>& arr, int low, int high) {
    int pivot = arr[high]; // 选择最后一个元素作为基准值
    int i = low - 1; // 小于基准值的元素的最右边界
    
    // 将小于基准值的元素放到左侧，大于等于基准值的元素放到右侧
    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    
    // 将基准值放到正确的位置上
    swap(arr[i + 1], arr[high]);
    return i + 1;
}

void quickSort(vector<int>& arr, int low, int high) {
    if (low < high) {
        // 划分数组，获取基准值的位置
        int pi = partition(arr, low, high);
        
        // 递归地对基准值左右两侧的子数组进行排序
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    vector<int> arr = {64, 34, 25, 12, 22, 11, 90};
    
    cout << "原始数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;
    
    quickSort(arr, 0, arr.size() - 1);
    
    cout << "排序后的数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;
    
    return 0;
}

堆排序

堆排序是一种基于二叉堆数据结构的排序算法。它利用了堆的性质：在一个最大堆（或最小堆）中，父节点的值总是大于等于（或小于等于）其子节点的值。堆排序的基本思想可以概括为以下几个步骤：

构建最大堆： 将待排序的数组看作一个完全二叉树，并将其转换为最大堆。这一步通常从最后一个非叶子节点开始，依次向上调整，使得每个节点都满足堆的性质。
交换堆顶元素和末尾元素： 将堆顶元素（即最大值）与堆的最后一个元素进行交换，然后将堆的大小减1，即排除最大值所在的节点。
调整堆： 将交换后的堆重新调整为最大堆，即调用函数对堆进行下沉操作，以维持堆的性质。
重复步骤2和3： 重复执行步骤2和3，直到堆的大小减小为1，即所有元素都已经有序。

堆排序的时间复杂度为 O(n log n)，其中 n 是数组的大小。虽然堆排序不是稳定的排序算法，但是它是一种原地排序算法，不需要额外的存储空间。

#include <iostream>
#include <vector>
using namespace std;

// 调整堆，使以节点 i 为根的子树满足最大堆性质
void maxHeapify(vector<int>& arr, int n, int i) {
    int largest = i; // 初始化根节点为最大值
    int left = 2 * i + 1; // 左孩子节点的索引
    int right = 2 * i + 2; // 右孩子节点的索引

    // 找出根节点、左孩子节点和右孩子节点中的最大值
    if (left < n && arr[left] > arr[largest])
        largest = left;
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // 如果最大值不是根节点，则交换根节点和最大值节点，然后递归调整交换后的子树
    if (largest != i) {
        swap(arr[i], arr[largest]);
        maxHeapify(arr, n, largest);
    }
}

// 堆排序
void heapSort(vector<int>& arr) {
    int n = arr.size();

    // 构建最大堆
    for (int i = n / 2 - 1; i >= 0; i--)
        maxHeapify(arr, n, i);

    // 依次取出堆顶元素（最大值），然后调整堆
    for (int i = n - 1; i > 0; i--) {
        swap(arr[0], arr[i]); // 将堆顶元素（最大值）放到数组末尾
        maxHeapify(arr, i, 0); // 调整堆，保持堆的性质
    }
}

int main() {
    vector<int> arr = {64, 34, 25, 12, 22, 11, 90};

    cout << "原始数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    heapSort(arr);

    cout << "排序后的数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    return 0;
}

计数排序

统计元素出现次数： 遍历待排序数组，统计每个元素出现的次数，通常需要额外的空间来存储这些统计信息。
累计出现次数： 对统计数组进行累加，以便确定每个元素在有序序列中的位置。
重构有序序列： 根据统计信息，重新构建有序序列，将每个元素放置到正确的位置上。

计数排序的时间复杂度为 O(n+k)，其中 n 是数组的大小，k 是待排序数组中的最大值和最小值的差值。计数排序适用于待排序的元素都是非负整数，并且数值范围不是特别大的情况下，因为需要额外的空间来存储统计信息。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

void countingSort(vector<int>& arr) {
    int max_val = *max_element(arr.begin(), arr.end()); // 获取数组中的最大值
    int min_val = *min_element(arr.begin(), arr.end()); // 获取数组中的最小值

    int range = max_val - min_val + 1; // 计算数值范围

    // 创建计数数组，并初始化为0
    vector<int> count(range, 0);

    // 统计每个元素的出现次数
    for (int num : arr) {
        count[num - min_val]++;
    }

    // 根据统计信息，重新构建有序序列
    int index = 0;
    for (int i = 0; i < range; i++) {
        while (count[i] > 0) {
            arr[index++] = i + min_val;
            count[i]--;
        }
    }
}

int main() {
    vector<int> arr = {4, 2, 2, 8, 3, 3, 1};

    cout << "原始数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    countingSort(arr);

    cout << "排序后的数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    return 0;
}

桶排序

将元素分配到桶中： 遍历待排序数组，根据元素的值将其分配到对应的桶中。为了使桶排序更加均匀，通常会根据元素的值范围和桶的数量进行合适的划分。
对每个桶中的元素进行排序： 对每个非空的桶中的元素进行排序，可以选择任何一种排序算法，通常使用插入排序或者快速排序。
合并桶中的元素： 将每个桶中的元素按照顺序合并起来，形成有序序列。

桶排序的时间复杂度取决于对每个桶中的元素进行排序所使用的算法，通常情况下是 O(n+k)，其中 n 是数组的大小，k 是桶的数量。桶排序适用于待排序的元素均匀分布在某个区间内的情况，例如在小范围内的浮点数排序。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

void bucketSort(vector<int>& arr, int bucketSize) {
    if (arr.empty()) return;

    int min_val = *min_element(arr.begin(), arr.end());
    int max_val = *max_element(arr.begin(), arr.end());

    // 计算桶的数量
    int bucketCount = (max_val - min_val) / bucketSize + 1;

    // 创建桶并初始化为空
    vector<vector<int>> buckets(bucketCount);

    // 将元素分配到桶中
    for (int num : arr) {
        int index = (num - min_val) / bucketSize;
        buckets[index].push_back(num);
    }

    // 对每个桶中的元素进行排序（可以选择任何一种排序算法）
    for (auto& bucket : buckets) {
        sort(bucket.begin(), bucket.end());
    }

    // 合并桶中的元素
    int index = 0;
    for (const auto& bucket : buckets) {
        for (int num : bucket) {
            arr[index++] = num;
        }
    }
}

int main() {
    vector<int> arr = {29, 25, 35, 49, 47, 5, 21, 39, 33};

    cout << "原始数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    bucketSort(arr, 10);

    cout << "排序后的数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    return 0;
}

基数排序

获取数字的最大位数： 首先，我们需要找出待排序数组中的最大数字，并确定它的位数。
按位进行计数排序： 从个位开始，依次对每一位进行计数排序。在计数排序过程中，我们需要获取每个数字的当前位数的值，并根据这个值将数字放入对应的桶中。
重复计数排序： 对于每一位数，都需要进行一次计数排序。我们可以通过循环来实现这个过程，直到所有位数都被考虑过。

基数排序的时间复杂度为 O(nk)，其中 n 是数组的大小，k 是数字的最大位数。虽然基数排序对于大数值范围的数组来说可能会占用较多的空间，但它在时间复杂度上有着稳定的性能。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 获取数字的最大位数
int getMaxDigit(int num) {
    int digit = 0;
    while (num != 0) {
        num /= 10;
        digit++;
    }
    return digit;
}

// 获取数字的指定位数的值
int getDigit(int num, int digit) {
    while (digit > 1) {
        num /= 10;
        digit--;
    }
    return num % 10;
}

void countingSort(vector<int>& arr, int exp) {
    int n = arr.size();
    vector<int> output(n), count(10, 0);

    // 统计每个数字出现的次数
    for (int num : arr) {
        int digit = getDigit(num, exp);
        count[digit]++;
    }

    // 计算累积次数
    for (int i = 1; i < 10; i++) {
        count[i] += count[i - 1];
    }

    // 根据统计信息，将数字放入输出数组中
    for (int i = n - 1; i >= 0; i--) {
        int digit = getDigit(arr[i], exp);
        output[count[digit] - 1] = arr[i];
        count[digit]--;
    }

    // 将输出数组复制到原始数组中
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];
    }
}

void radixSort(vector<int>& arr) {
    int maxDigit = getMaxDigit(*max_element(arr.begin(), arr.end()));

    // 对每一位进行计数排序
    for (int exp = 1; maxDigit / exp > 0; exp *= 10) {
        countingSort(arr, exp);
    }
}

int main() {
    vector<int> arr = {170, 45, 75, 90, 802, 24, 2, 66};

    cout << "原始数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    radixSort(arr);

    cout << "排序后的数组为: ";
    for (int num : arr)
        cout << num << " ";
    cout << endl;

    return 0;
}

海报

海报图正在生成中...

竖版宽版

免责声明：本站除原创代码外的资源均收集于网络，不保证代码的完整性和可用性，只做学习和交流使用，版权归原作者所有，请在下载后24小时之内自觉删除。若作商业用途，请购买正版，由于未及时购买正版授权发生的侵权行为，与本站无关。本站的内容如果侵犯了您的权益，请及时告知我们，我们即刻处理！
少儿编程课程儿童编程教育编程启蒙班青少年编程培训 Scratch编程学习 Python少儿编程机器人编程教育编程思维训练编程游戏化教学在线少儿编程平台儿童编程软件推荐编程竞赛准备编程兴趣班逻辑思维与编程少儿编程教材编程与STEM教育编程技能培养编程语言入门（如：JavaScript少儿版）家长如何选择少儿编程课编程对孩子未来的影响编程项目实践编程与创造力培养编程思维在日常生活中的应用编程教育专家观点编程教育趋势分析少儿编程社区编程夏令营编程冬令营编程学习路线图编程证书考试少儿编程启蒙儿童图形化编程（如Scratch编程）青少年Python编程编程基础班（针对小学生）编程进阶课程（适合高年级学生）机器人编程工作坊 AI启蒙编程课逻辑思维编程游戏编程与数学能力提升编程思维训练营编程解决问题的能力培养在线互动编程课堂编程项目实战演练编程创意工坊编程教育APP推荐编程教育论坛与社区编程兴趣小组编程竞赛辅导编程证书考试准备编程教育政策解读编程教育家长指南编程与跨学科学习（STEM/STEAM）编程与创新能力培养编程与未来职业规划编程教育师资培训编程教育研究成果分享编程教育行业标准编程教育市场动态编程教育投资前景编程教育公益项目
微点点-专业的知识付费平台 » C++ 排序算法（基本）

C++ 排序算法（基本）

冒泡排序

选择排序

插入排序

希尔排序

归并排序

快速排序

堆排序

计数排序

桶排序

基数排序

admin 普通

发表回复取消回复

冒泡排序

选择排序

插入排序

希尔排序

归并排序

快速排序

堆排序

计数排序

桶排序

基数排序

admin 普通

相关推荐

发表回复 取消回复

提供最优质的资源集合

欢迎给我们留言 +—

发表回复取消回复